When to use
Find targetValue in sorted array
Algorithm
Recursive approach
1. StartIndex = 0 (lower bound), endIndex = arr.length (upper bound), midIndex = starIndex + endIndex / 2,
2. Recursion until (startIndex > endIndex (Not found))
. arr[midIndex] == targetValue ? => return midIndex
.arr[midIndex] > targetValue ? => endIndex = mid – 1 (targetValue on left side)
.arr[midIndex] < targetValue ? => startIndex = mid + 1 (targetValue on right side)
Recursive call BinarySearch(startIndex, endIndex, targetValue)
Iterative approach
1. StartIndex = 0 (lower bound), endIndex = arr.length (upper bound), midIndex = starIndex + endIndex / 2,
2. Recursion until (startIndex != endIndex (Not found))
. arr[midIndex] == targetValue ? => return midIndex
.arr[midIndex] > targetValue ? => endIndex = mid – 1 (targetValue on left side)
.arr[midIndex] < targetValue ? => startIndex = mid + 1 (targetValue on right side)
3. if not return in 2.
return -1 (not found)
Time Complexity
O(log N)
Kotlin example
Binary Search index (no duplicates)
정확히 특정 값이 존재하는 index 를 찾는다.
값이 존재하지 않으면 - 1을 리턴한다.
class BinarySearch {
// Find index in sorted array (no duplicates)
fun binarySearch(arr: IntArray, targetValue: Int) : Int {
var startIdx = 0
var endIdx = arr.lastIndex
while (startIdx <= endIdx) {
val midIdx = (startIdx + endIdx) / 2
if (arr[midIdx] < targetValue) startIdx = midIdx + 1
else if (arr[midIdx] > targetValue) endIdx = midIdx - 1
else return midIdx
}
// not found
return -1
}
@Test
internal fun testBinarySearch() {
val oddNums = intArrayOf(1, 3, 5, 7, 9, 11, 13)
assertEquals(2, binarySearch(oddNums, 5))
assertEquals(oddNums.lastIndex - 1, binarySearch(oddNums, 11))
assertEquals(-1, binarySearch(oddNums, 4))
}
}
Lower bound , Upper bound in Binary Search
중복이 허용된 배열에서는
이분 탐색을 쓸 방법이 없을까?
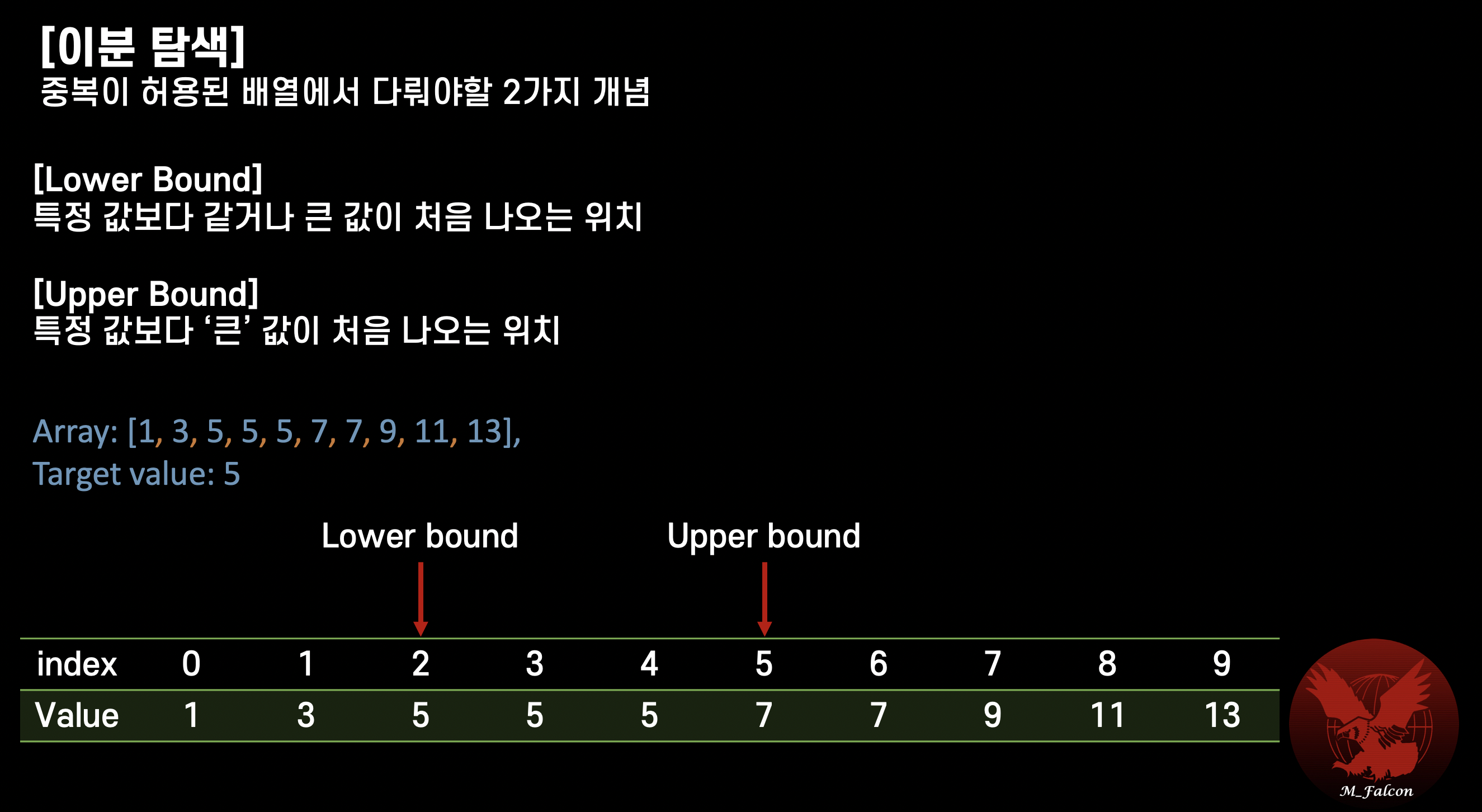
Find lower bound index
원소가 배열안에 중복된 경우, 같거나 큰 값이 처음 나오는 index 를 찾는다.
원소가 존재하지 않으면 배열의 크기가 리턴된다.
class BinarySearch {
// Find lower bound index in sorted array (duplicates)
// lowerBound
fun binarySearchLowerBound(arr: IntArray, targetValue: Int): Int {
var startIdx = 0
// 배열 범위를 넘은 큰 범위가 있는 경우
// 찾고자 하는 원소가 있어야할 위치는 배열의 크기 (마지막 인덱스 + 1) 이다.
var endIdx = arr.size
// <= 이 아니라 < 인 것은 직접 그림을 그려봐야 안다.
while (startIdx < endIdx) {
val midIdx = (startIdx + endIdx) / 2
if (arr[midIdx] < targetValue) startIdx = midIdx + 1
if (arr[midIdx] >= targetValue) endIdx = midIdx
}
// if not found return arr size
// found -> lower bound
return endIdx
}
@Test
internal fun testBinarySearchLowerBound() {
val oddNumsWithDuplicates = intArrayOf(1, 3, 5, 5, 5, 7, 7, 9, 11, 13)
assertEquals(2, binarySearchLowerBound(oddNumsWithDuplicates, 5))
assertEquals(2, binarySearchLowerBound(oddNumsWithDuplicates, 4))
}
}
Find upper bound index
원소가 배열안에 중복된 경우, 큰 값이 처음 나오는 index 를 찾는다.
원소가 존재하지 않으면 배열의 크기가 리턴된다.
class BinarySearch {
// Find upper bound index in sorted array (duplicates)
fun binarySearchUpperBound(arr: IntArray, targetValue: Int): Int {
var startIdx = 0
var endIdx = arr.size
while (startIdx < endIdx) {
val midIdx = (startIdx + endIdx) / 2
if (arr[midIdx] <= targetValue) startIdx = midIdx + 1
if (arr[midIdx] > targetValue) endIdx = midIdx
}
// if not found return arr size
// found -> upper bound
return startIdx
}
@Test
internal fun testBinarySearchUpperBound() {
val oddNumsWithDuplicates = intArrayOf(1, 3, 5, 5, 5, 7, 7, 9, 11, 13)
assertEquals(5, binarySearchUpperBound(oddNumsWithDuplicates, 5))
assertEquals(5, binarySearchUpperBound(oddNumsWithDuplicates, 6))
assertEquals(oddNumsWithDuplicates.size, binarySearchUpperBound(oddNumsWithDuplicates, 14))
}
}
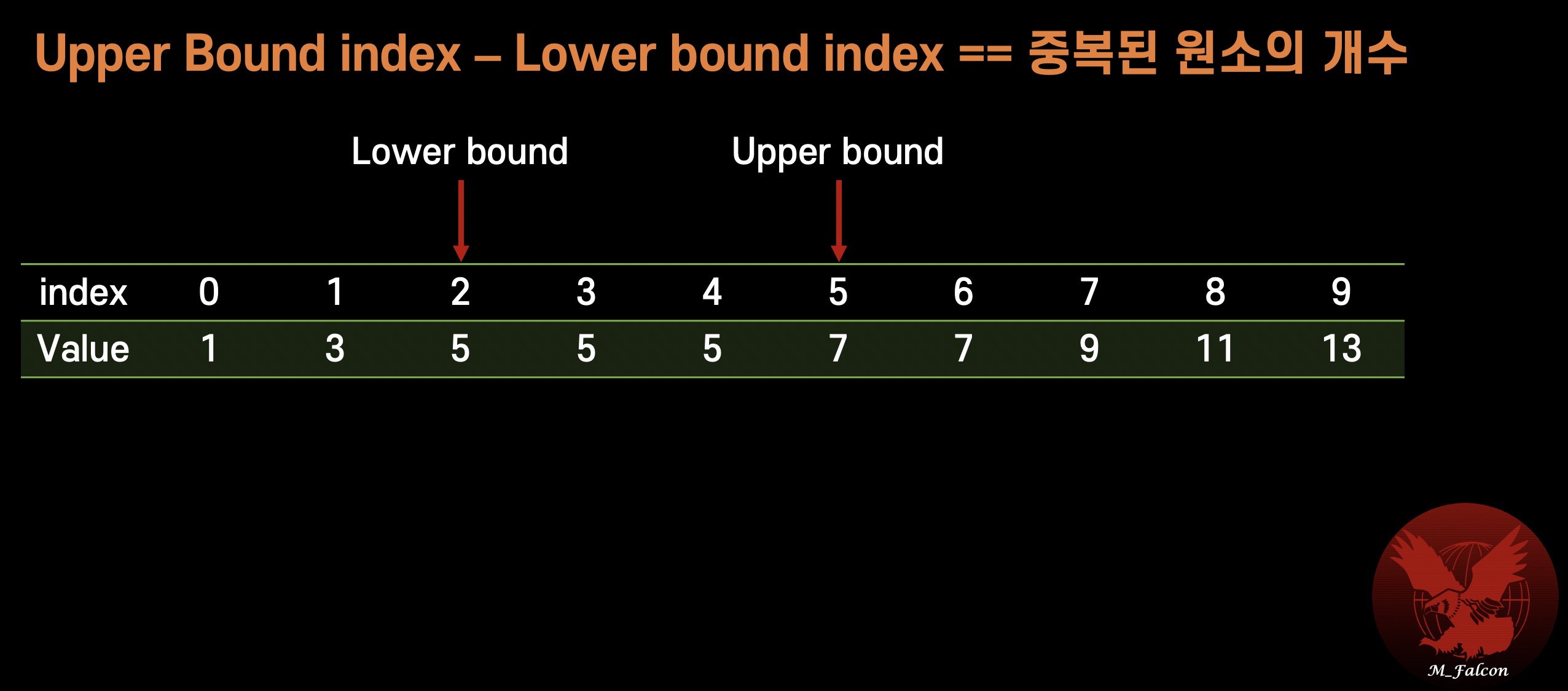
Lower bound && Upper bound 를 왜 알아야하나?
이분탐색을 통해 중복된 원소 갯수를 아는데 매우 유용하다. (값의 존재 범위를 알 수 있다.)
Kotlin 에 내장된 binary search
Array.binarySearch(element, fromIndex, endIndex) 를 제공한다.
오름차순으로 정렬된 배열을 input 으로 가정한다.
중복이 허용된 배열에서는 반환하는 인덱스가 불규칙하므로 위의 lower bound + upper bound 커스텀 메소드를 직접 작성하는게 낫다.
반면에, 중복이 없는 경우 원하는 값을 찾지 못했을 때도 -(위치했어야할 인덱스 + 1) 를 리턴하므로 이해하고 사용하면
직접 binary search 메소드를 쓰지 않고도 편하게 사용할 수 있다.
@Test
internal fun testBinarySearchInternalKotlin() {
val oddNumsWithDuplicates = intArrayOf(1, 3, 5, 5, 5, 7, 7, 9, 11, 13)
// 배열 내에 존재하지 않는 원소인 경우 음수 리턴.
// 있어야할 위치는 '5' 이므로 음수 값에 -1 을 더해 '-6' 리턴 (존재하지 않음을 음수로 표현)
assertEquals(-6, oddNumsWithDuplicates.binarySearch(6))
// 중복이 있을 때 존재하는 원소의 index 값은 무작위므로
// lower bound, upper bound 가 필요할 경우 , 중복이 있는 배열인 경우 커스텀 함수를 직접 작성하는게 낫다.
// 14가 존재하지 않으므로 배열 크기인 -(10 + 1) 리턴
assertEquals(-(oddNumsWithDuplicates.size + 1), oddNumsWithDuplicates.binarySearch(14))
// 0이 있어야할 자리는 0 이지만 실제로 존재하지 않으므로 -(0 + 1) 리턴
assertEquals(-(0 + 1), oddNumsWithDuplicates.binarySearch(0))
}
국룰은 오름차순 배열에 쓰는 것이지만,
내림차순으로 정렬하고 Comparator 를 2번째 인자로 넘기면 내림차순 배열에 대해서도 값 찾기가 가능하다.
@Test
internal fun testBinarySearchDescending() {
val descendingArr = intArrayOf(1, 3, 5, 5, 5, 7, 7, 9, 11, 13).sortedDescending()
println(descendingArr) // [13, 11, 9, 7, 7, 5, 5, 5, 3, 1]
// 1st: target Element
// 2nd: Comparator (내림차순인 경우)
// Comparator 를 명시하려면 IntArray 가 아닌 List<Int> 컬렉션에서 사용 가능하다.
assertEquals(2, descendingArr.binarySearch (9, { a, b->b.compareTo(a)}))
val ascendingArr = intArrayOf(1, 3, 5, 5, 5, 7, 7, 9, 11, 13).sorted()
// 오름차순 배열을 두고 내림차순을 comparator 로 넘길 경우
// Not found
assertEquals(-1, ascendingArr.binarySearch (9, {a,b -> b.compareTo(a)}))
}
알고리즘 문제 풀이시
내장된 메소드보다
binary search 를 직접 구현해서 쓰는게 더 낫다.
(실수 확률 적고, 중복 원소 처리 가능)
🔗 Reference
Binary Search - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
Lower bound basics
Efficient find in a sorted range Introduction We’re going to have a look at a function similar to std::lower_bound from the standard C++ library with some differences. The name lower_bound is easier to understand if we look at equal_range and upper_bound
bajamircea.github.io
binarySearch - Kotlin Programming Language
kotlinlang.org
'Algorithm > Algorithm (이론)' 카테고리의 다른 글
| [Algorithm] 재귀 (0) | 2022.09.07 |
|---|---|
| [Algorithm] BFS (0) | 2022.09.02 |
| [Data Structure] Binary Search Tree (0) | 2021.03.01 |
| [Algorithm] Dijkstra (0) | 2021.02.14 |
| [Algorithm] Heap Sort (0) | 2021.02.11 |