구현 방식
2가지
1. Priority Queue.
// O(n log n)
for(int i = 1; i <= size; i ++) {
prirorityQueue.insert(i);
}
// O(n log n)
for(int i = 1; i <= size; i++) {
arr[i] = priorityQueue.getMax();
cout << arr[i] << " ";
}
Prirority Queue의 모든 연산은 O(log n) 임을 알고있다.
Prirority Queue 기본 연산 구현은 여기
2. BuildHeap + ShiftDown
이 방식은 무작위 값이 들어있는 배열을 Binary Heap으로 전환한 후
루트 노드와 맨 끝노드를 스왑하여 루트 노드를 끌어내리며 정렬하는 정렬하는 방식이다.
⚠️ 3가지 주의할 점이 있다.
1. 루프를 거듭하며 맨 마지막 노드는 범위에서 제외시킬 것.
2. 오름 차순을 원한다면 maxHeap, 내림 차순을 원한다면 minHeap 으로 힙을 먼저 생성할 것.
3. 루프 범위 & 순서는 맨끝 노드에서 루트 노드 직전까지.
// (convert array to MaxHeap)
buildHeap{
for(int i = n/2; i>= ; i--) {
shiftDown(i);
}
}
//Time Complexity : O(n) // 2n
HeapSort {
buildHeap(); // 2n
// O(n log n)
for (int i = size; i > rootIndex; i--) { // N
swap(arr[i], arr[rootIndex]);
shiftDown(rootIndex); // log N
}
}
Time Complexity
(1) Prirority Queue == n log n + n log n => O(n * log n)
(2) Build Heap + ShiftDown == 2n + n log n => O(n * log n)
∴ O (n * log n)
BuildHeap Analysis
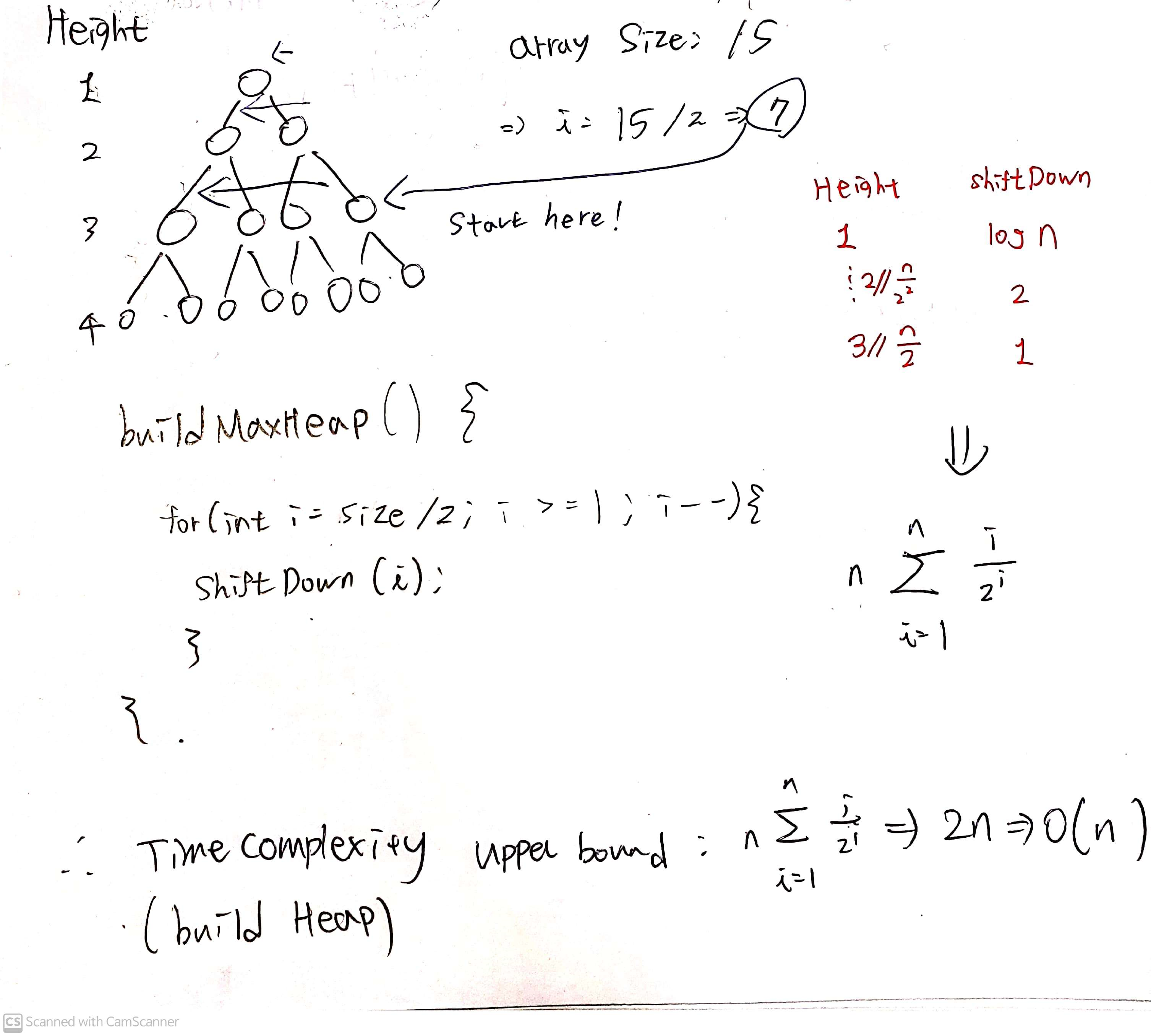
When to use?
k Largest(Smallest) elements in array
Implementation (C++)
// make Max Heap
void PriorityQueue::shiftDown(int index) {
int maxIndex = index;
do {
index = maxIndex;
const int leftChildIndex = getLeftChildIndex(index);
const int rightChildIndex = getRightChildIndex(index);
if (leftChildIndex <= size && heapArray[maxIndex] < heapArray[leftChildIndex]) maxIndex = leftChildIndex;
if (rightChildIndex <= size && heapArray[maxIndex] < heapArray[rightChildIndex]) maxIndex = rightChildIndex;
std::swap(heapArray[index], heapArray[maxIndex]);
// already find correct index -> finish
} while (maxIndex != index);
}
void PriorityQueue::buildHeap() {
for (int index = getSize() / 2; index >= 1 ; index--) {
shiftDown(index);
}
}
void PriorityQueue::heapSort() {
buildHeap();
//int index = getSize();
while (index > 1) {
//std::swap(heapArray[index--], heapArray[rootIndex]);
std::swap(heapArray[size--], heapArray[rootIndex]);
shiftDown(rootIndex);
}
}
⚠️ Mistake
void PriorityQueue::heapSort() {
buildHeap();
//int index = getSize();
while (index > 1) {
//std::swap(heapArray[index--], heapArray[rootIndex]);
std::swap(heapArray[size--], heapArray[rootIndex]);
shiftDown(rootIndex);
}
}주석 처리 된 부분을 보면 알 수 있듯이, 원소 갯수를 미리 keep하고 index를 줄이는 방법으로 구현했으나
맨 꼭대기에 올라갔던 노드가 내려오며 다시 꼴찌 자리로 돌아갈 수 있기 때문에 정확히 정렬되지 않는다.
아래 영상을 보면 왜 index가 아닌 해당 클래스의 배열 size를 직접 줄이며 정렬하는지 알 수 있다.
Reference
HeapSort - GeeksforGeeks
A Computer Science portal for geeks. It contains well written, well thought and well explained computer science and programming articles, quizzes and practice/competitive programming/company interview Questions.
www.geeksforgeeks.org
'Algorithm > Algorithm (이론)' 카테고리의 다른 글
| [Data Structure] Binary Search Tree (0) | 2021.03.01 |
|---|---|
| [Algorithm] Dijkstra (0) | 2021.02.14 |
| [Data Structure] Priority Queue (0) | 2021.02.10 |
| [Algorithm] Prim (feat. compare to Kruskal) (0) | 2021.02.10 |
| [Algorithm] Kruskal Algorithm (0) | 2021.02.07 |