비트마스킹 기법을 사용하기 위해 익혀야할 비트연산자를 정리해보자.
1. 길이 N을 갖는 이진수를 모두 1 (flag on) 상태로 만들기
표현식
$$ (2 << N) - 1 $$
@Test
internal fun turOnAllFlags() {
// 총 N 길이를 갖는 모든 flag 를 1 상태로 시작하고 싶다.
// ex) 5자리 flag 를 모두 1 => 11111
// 십진수로는 2 ^ N - 1 로 표현가능하다.
// 2 ^ 6 - 1 == 63
val num = (1 shl (5 + 1)) - 1
println("=============")
println("All flag on")
println(toDecimalString(num))
println(toBinaryString(num))
println("=============")
}결과

2. 특정 index flag bit 키기
표현식
$$ num\; or \; (1 << index) $$
Kotlin Code
@Test
internal fun tunrOnIndexFlag() {
val num = 1 shl 4
println("=============")
println("Before")
println(toDecimalString(num))
println(toBinaryString(num))
println("=============")
// 2번째 flag (index 번호 2) 를 키고 싶다면
// 10100
val onFlagNum = num or (1 shl 2)
println("=============")
println("index 2 flag on")
println(toDecimalString(onFlagNum))
println(toBinaryString(onFlagNum))
println("=============")
}결과

3. 특정 index 플래그 on 인지 검사
표현식
num 은 검사할 숫자
$$ num\; and \; (1 << index) $$
결과가 0이 아닌 경우 flag on (true)
0 인 경우 flag off (false)
Kotlin Code
private fun isFlagOn(num: Int): Boolean {
if (num == 0) return false
return true
}
@Test
internal fun testCheckFlagOnIndex() {
// 11100
val num = (1 shl 4) or (1 shl 3) or (1 shl 2)
println("=============")
println("Before")
println(toDecimalString(num))
println(toBinaryString(num))
println("=============")
val index2 = 1 shl 2
val temp = num and index2
println("=============")
println(toDecimalString(index2))
println(toBinaryString(index2))
println("index 2 flag on")
println(isFlagOn(temp))
println("=============")
}결과

4. 길이 N 을 갖는 flag 비트 뒤집기
$$ num == (1 << N + 1) - 1 $$
num: 길이 N 을 갖는 모든 flag 가 켜져있는 숫자
ex) 길이가 5인 모든 flag on => 11111 == 2 ^ (5 + 1) - 1
표현식
위에서 구한 num을 활용한다.
$$ num\; and\; not\, targetNum $$
Kotlin Code
kotlin 에서는 .inv() 메소드를 사용해 비트를 뒤집을 수 있다.
not 연산자(~)는 안타깝게도 지원하지 않는다.
// 길이 N 을 갖는 이진수의 flag 비트를 뒤집기
// 0100 을 뒤집기 => 총 4자리를 갖고 모두 켜진 1111과 0100을 뒤집은 이진수 (111....1011) 를 AND 연산
// 결과 : 1011
@Test
internal fun testReverseFlag() {
// true <-> false switch
val N = (1 shl 4) - 1
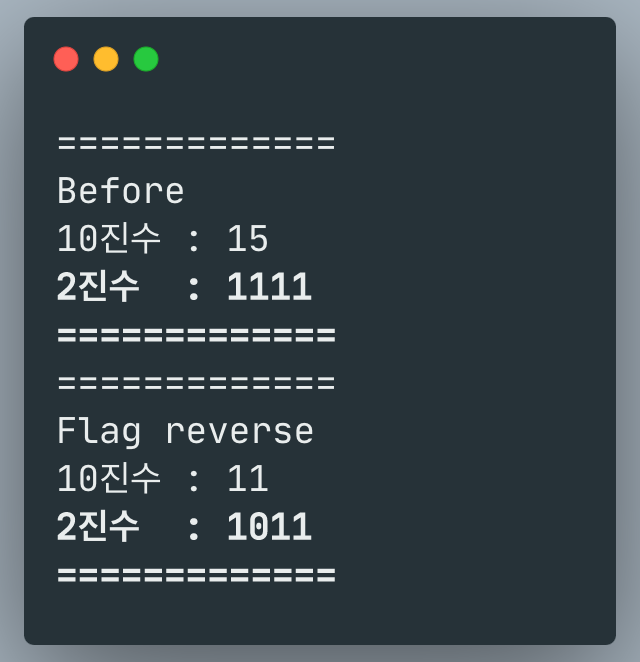
println("=============")
println("Before")
println(toDecimalString(N))
println(toBinaryString(N))
println("=============")
// kotlin 에서는 not 연산자를 지원하지 않고
// 비트 반전에 .inv() 메소드가 사용된다. (invert 의 약자)
val target = (1 shl 2).inv()
val result = N and target
println("=============")
println("Flag reverse")
println(toDecimalString(result))
println(toBinaryString(result))
println("=============")
}결과
5. 켜져있는 비트중 최하위 비트 (LSB) 찾기
표현식
$$ not\,x + 1 and x $$
최하위 비트 중 활성화된 비트를 찾기 위한 식이다.
이 식이 어디로부터 나왔는지는 직접 해봐야만 알 수있다.
표현식 변형
최초의 식을 더 간단하게 표현하기 위해 식을 변형해보자.
$$ \~x = -(x + 1) $$
$$ \~x + 1 == -x $$
$$ -x == ~x + 1 $$
Kotlin Code
표현식을 검증하기 위한 소스코드
@Test
internal fun testNotBit() {
val num = 15
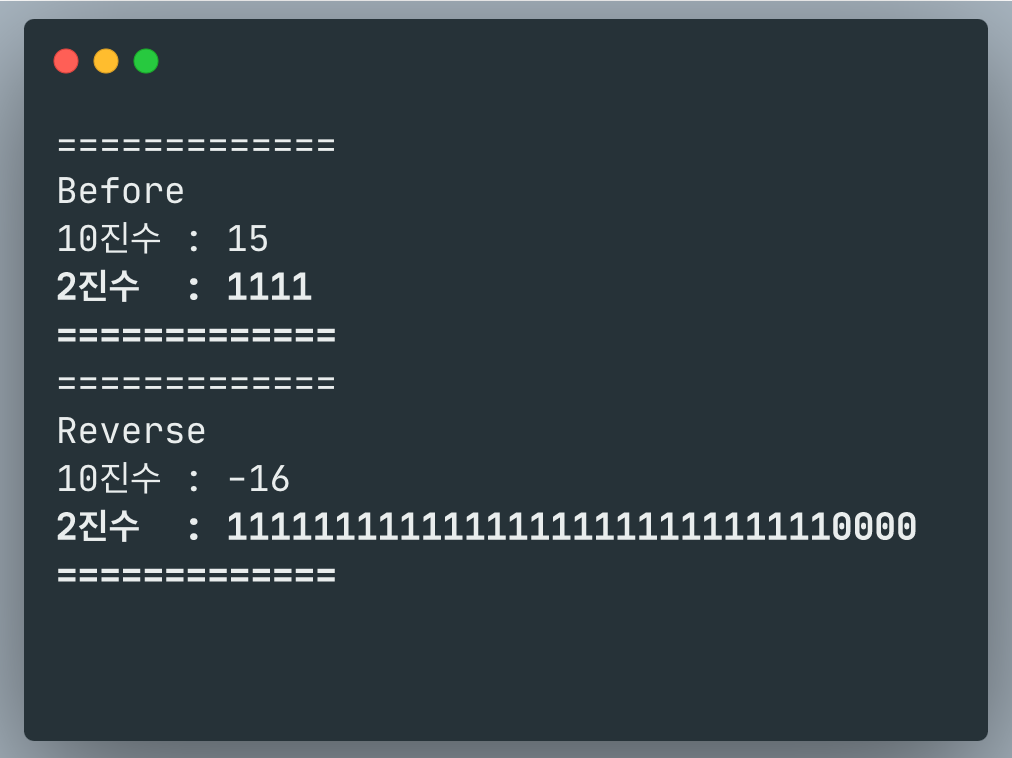
println("=============")
println("Before")
println(toDecimalString(num))
println(toBinaryString(num))
println("=============")
val negativeNum = - (num + 1)
println("=============")
println("Reverse")
println(toDecimalString(negativeNum))
println(toBinaryString(negativeNum))
println("=============")
// ~x == - (x + 1)
// 최하위 비트중 활성화된 값을 뽑기위한 식은 원래 ~x + 1 and x 이다.
// 위 결과로부터 ~x + 1 == -x 라는 식을 뽑아낼 수 있다.
// 부호 반전 이후에 + 1 하면 항상 최하위 비트(LSB) 중 활성화된 값을 뽑아낼 수 있다.
// 결론: 최하위 비트중 활성화된 값을 찾아내는 표현식은 다음과 같다.
// x and -x
}출력
📝 암기해야할 표현식
표현식 변형을 통해 결과적으로 우리가 찾는 LSB 는 다음 표현식으로 구할 수 있다.
$$ x\; and\; -x $$
// 가장 낮은 비트 중 flag 가 켜져있는 수 찾기
@Test
internal fun testFindTrueLSB() {
val num = (1 shl 3) or (1 shl 2)
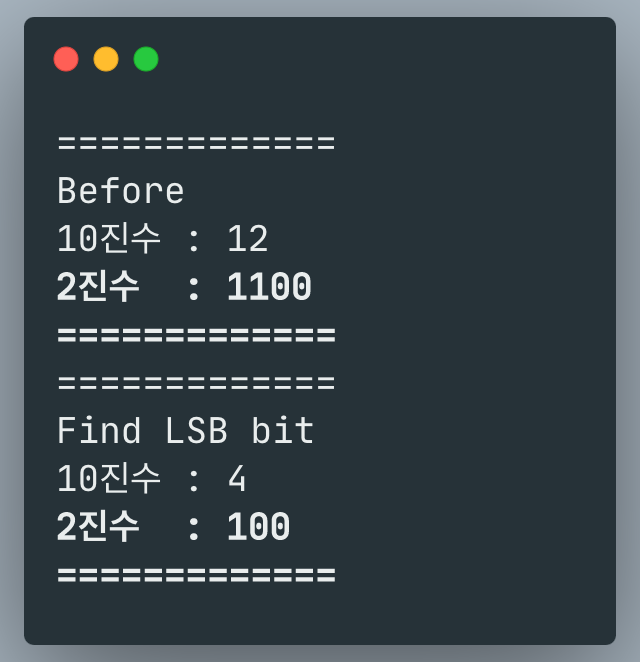
println("=============")
println("Before")
println(toDecimalString(num))
println(toBinaryString(num))
println("=============")
// LSB 찾기는 (x & -x) 표현식을 암기해도 좋다.
val result = num and (-num)
println("=============")
println("Find LSB bit")
println(toDecimalString(result))
println(toBinaryString(result))
println("=============")
}
결과
6. XOR
서로 값이 다른 경우에만 true(1) , 같으면 false (0)을 출력한다.
표현식
$$ a\, xor\, b $$
Kotlin Code
@Test
internal fun testXOR() {
// val num = 110110
val num = 54
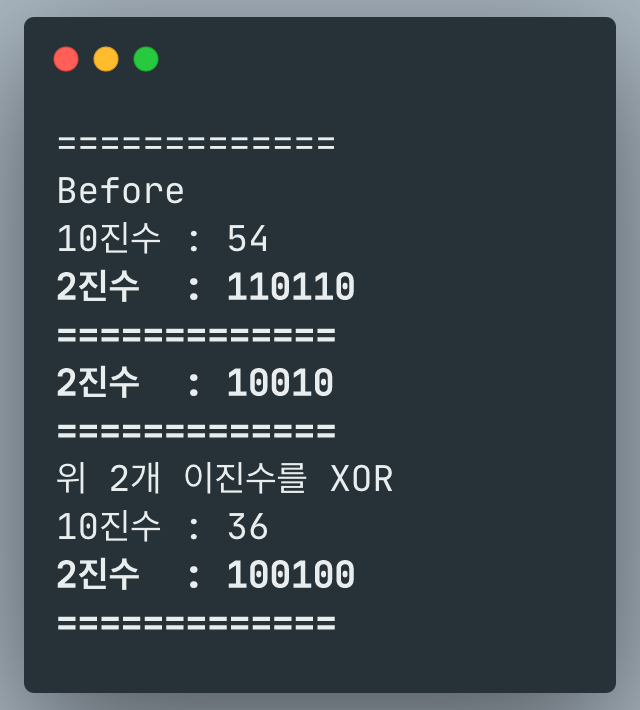
println("=============")
println("Before")
println(toDecimalString(num))
println(toBinaryString(num))
println("=============")
// 010010
val dividend = 18
println(toBinaryString(dividend))
val result = num xor dividend
println("=============")
println("위 2개 이진수를 XOR")
println(toDecimalString(result))
println(toBinaryString(result))
println("=============")
}결과
전체 소스코드
import org.junit.jupiter.api.Test
class BitMasking {
private fun toDecimalString(num: Int) : String {
return "10진수 : $num"
}
private fun toBinaryString(num: Int) : String {
return "2진수 : ${Integer.toBinaryString(num)}"
}
private fun isFlagOn(num: Int): Boolean {
if (num == 0) return false
return true
}
@Test
internal fun turOnAllFlags() {
// 총 N 길이를 갖는 모든 flag 를 1 상태로 시작하고 싶다.
// ex) 5자리 flag 를 모두 1 => 11111
// 십진수로는 2 ^ N - 1 로 표현가능하다.
// 2 ^ 6 - 1 == 63
val num = (1 shl (5 + 1)) - 1
println("=============")
println("All flag on")
println(toDecimalString(num))
println(toBinaryString(num))
println("=============")
}
@Test
internal fun tunrOnIndexFlag() {
val num = 1 shl 4
println("=============")
println("Before")
println(toDecimalString(num))
println(toBinaryString(num))
println("=============")
// 2번째 flag (index 번호 2) 를 키고 싶다면
// 10100
val onFlagNum = num or (1 shl 2)
println("=============")
println("index 2 flag on")
println(toDecimalString(onFlagNum))
println(toBinaryString(onFlagNum))
println("=============")
}
@Test
internal fun testCheckFlagOnIndex() {
// val num = (1 shl 4) - 1
// val num = (1 shl 4)
val num = (1 shl 4) or (1 shl 3) or (1 shl 2)
println("=============")
println("Before")
println(toDecimalString(num))
println(toBinaryString(num))
println("=============")
val index2 = 1 shl 2
val temp = num and index2
println("=============")
println(toDecimalString(index2))
println(toBinaryString(index2))
println("index 2 flag on")
println(isFlagOn(temp))
println("=============")
}
// 길이 N 을 갖는 이진수의 flag 비트를 뒤집기
// 0100 을 뒤집기 => 총 4자리를 갖고 모두 켜진 1111과 0100을 뒤집은 이진수 (111....1011) 를 AND 연산
// 결과 : 1011
@Test
internal fun testReverseFlag() {
// true <-> false switch
val N = (1 shl 4) - 1
println("=============")
println("Before")
println(toDecimalString(N))
println(toBinaryString(N))
println("=============")
// kotlin 에서는 not 연산자를 지원하지 않고
// 비트 반전에 .inv() 메소드가 사용된다. (invert 의 약자)
val target = (1 shl 2).inv()
val result = N and target
println("=============")
println("Flag reverse")
println(toDecimalString(result))
println(toBinaryString(result))
println("=============")
}
@Test
internal fun testNotBit() {
val num = 15
println("=============")
println("Before")
println(toDecimalString(num))
println(toBinaryString(num))
println("=============")
val negativeNum = - (num + 1)
println("=============")
println("Reverse")
println(toDecimalString(negativeNum))
println(toBinaryString(negativeNum))
println("=============")
// ~x == - (x + 1)
// 최하위 비트중 활성화된 값을 뽑기위한 식은 원래 ~x + 1 and x 이다.
// 위 결과로부터 ~x + 1 == -x 라는 식을 뽑아낼 수 있다.
// 부호 반전 이후에 + 1 하면 항상 최하위 비트(LSB) 중 활성화된 값을 뽑아낼 수 있다.
// 결론: 최하위 비트중 활성화된 값을 찾아내는 표현식은 다음과 같다.
// x and -x
}
// 가장 낮은 비트 중 flag 가 켜져있는 수 찾기
@Test
internal fun testFindTrueLSB() {
val num = (1 shl 3) or (1 shl 2)
println("=============")
println("Before")
println(toDecimalString(num))
println(toBinaryString(num))
println("=============")
// LSB 찾기는 (x & -x) 표현식을 암기해도 좋다.
val result = num and (-num)
println("=============")
println("Find LSB bit")
println(toDecimalString(result))
println(toBinaryString(result))
println("=============")
}
@Test
internal fun testXOR() {
// val num = 110110
val num = 54
println("=============")
println("Before")
println(toDecimalString(num))
println(toBinaryString(num))
println("=============")
// 010010
val dividend = 18
println(toBinaryString(dividend))
val result = num xor dividend
println("=============")
println("위 2개 이진수를 XOR")
println(toDecimalString(result))
println(toBinaryString(result))
println("=============")
}
}'Algorithm > Algorithm (이론)' 카테고리의 다른 글
| Modular 연산 (0) | 2022.11.11 |
|---|---|
| [Algorithm] Parametric Search (0) | 2022.11.11 |
| [Algorithm] 2차원 배열 (행렬) 회전하기 (2) | 2022.10.05 |
| [Algorithm] 순열 조합 (0) | 2022.09.19 |
| [Algorithm] 재귀 (0) | 2022.09.07 |
